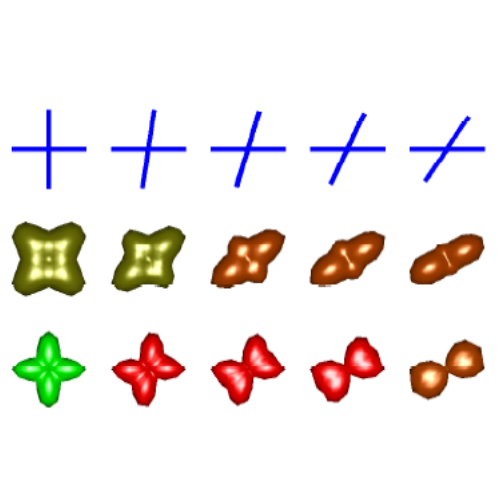Symmetric positive-definite Cartesian tensor fiber orientation distributions (CT-FOD)

by Weldeselassie, Y. | Barmpoutis, A. | Atkins, S.

Medical Image Analysis, vol. 16(6), August, 2012, pp. 1121-1129. https://doi.org/10.1016/j.media.2012.07.002

Category:
FacebookXEmailLinkedin

Description

A novel method for estimating a field of fiber orientation distribution (FOD) based on signal de-convolution from a given set of diffusion weighted magnetic resonance (DW-MR) images is presented. We model the FOD by higher order Cartesian tensor basis using a parametrization that explicitly enforces the positive semi-definite property to the computed FOD. The computed Cartesian tensors, dubbed Cartesian Tensor-FOD (CT-FOD), are symmetric positive semi-definite tensors whose coefficients can be efficiently estimated by solving a linear system with non-negative constraints. Next, we show how to use our method for converting higher-order diffusion tensors to CT-FODs, which is an essential task since the maxima of higher-order tensors do not correspond to the underlying fiber orientations. Finally, we propose a diffusion anisotropy index computed directly from CT-FODs using higher order tensor distance measures thus consolidating the whole analysis pipeline of diffusion imaging solely using CT-FODs. We evaluate our method qualitatively and quantitatively using simulated DW-MR images, phantom images, and human brain real dataset. The results conclusively demonstrate the superiority of the proposed technique over several existing multifiber reconstruction methods.

Additional information

Author

Weldeselassie, Y., Barmpoutis, A., Atkins, S.
Journal

Medical Image Analysis
Volume

16
Number

6
Year

2012
Month

August
Pages

1121-1129
DOI

https://doi.org/10.1016/j.media.2012.07.002

Citation

Citation

Weldeselassie, Y., Barmpoutis, A. and Atkins, S., 2012. Symmetric positive-definite Cartesian tensor fiber orientation distributions (CT-FOD). Medical Image Analysis, vol. 16(6), pp. 1121-1129. https://doi.org/10.1016/j.media.2012.07.002

BibTex

@article{digitalWorlds:153,
doi = {https://doi.org/10.1016/j.media.2012.07.002},
author = {Weldeselassie, Y.  and  Barmpoutis, A.  and  Atkins, S.},
title = {Symmetric positive-definite Cartesian tensor fiber orientation distributions (CT-FOD)},
journal = {Medical Image Analysis},
month = {August},
volume = {16},
number = {6},
year = {2012},
pages = {1121-1129}
}

See also…